Image Sharpening with a Laplacian Kernel

QUESTION: I'd like to see more fine detail in my image. Someone told me of a technique called "image sharpening" that may be the answer to my prayers. They say I need to use a Laplacian operator. What in the world is that? And is there any chance I can do this in IDL?

ANSWER: Your friend has probably been reading the excellent book, Digital Image Processing, Second Edition by Gonzales and Woods. It is a book well worth picking up if you plan to do any image processing in IDL. And, yes, you can do this kind of thing in IDL. Let me show you how.

Image sharpening falls into a category of image processing called spacial filtering. One can take advantage of how quickly or abruptly gray-scale values or colors change from one pixel to the next. First order operators (using first derivative measurements) are particularly good at finding edges in images. The Sobel and Roberts edge enhancement operators in IDL are examples of these first order filters, sometimes called gradient filters.

The Laplacian operator is an example of a second order or second derivative method of enhancement. It is particularly good at finding the fine detail in an image. Any feature with a sharp discontinuity (like noise, unfortunately) will be enhanced by a Laplacian operator. Thus, one application of a Laplacian operator is to restore fine detail to an image which has been smoothed to remove noise. (The median operator is often used to remove noise in an image.)

Consider the original 2D byte value image below, which is provided courtesy of NASA. This view of the Moon's north pole is a mosaic assembled from 18 images taken by Galileo's imaging system as the spacecraft flew by on December 7, 1992. The same image is found on page 130 of Gonzalez and Woods.

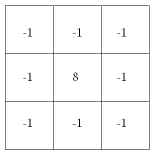
The Laplacian operator is implemented in IDL as a convolution between an image and a kernel. The Convol function is used to perform the convolution. The Laplacian kernel can be constructed in various ways, but we will use the same 3-by-3 kernel used by Gonzalez and Woods, and shown in the figure below.

In image convolution, the kernel is centered on each pixel in turn, and the pixel value is replaced by the sum of the kernel mutipled by the image values. In the particular kernel we are using here, we are counting the contributions of the diagonal pixels as well as the orthogonal pixels in the filter operation. This is not always necessary or desirable, although it works well here.

The Laplacian kernel is constructed in IDL like this:

   IDL> kernel = Replicate(-1, 3, 3)
   IDL> kernel[1,1] = 8
   IDL> Print, kernel
       -1       -1       -1
       -1        8       -1
       -1       -1       -1

We apply the convolution kernel to the image and display the filtered image like this:

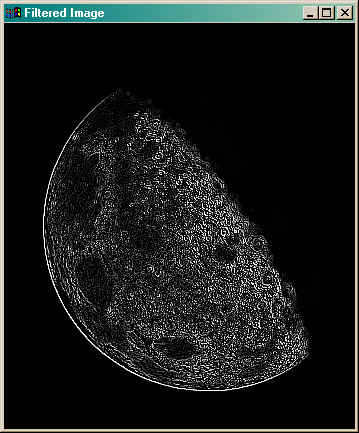
   IDL> filtered = Convol(image, kernel, Center=1)
   IDL> TV, filtered

The results are shown in the figure below.

Note the amount of fine detail found in the image with this filter. What we want to do is add this information back into the original image in order to sharpen the image. To do this properly, we have to scale the filtered data into the same 0 to 255 values of the original image.

It took me a while to understand this step in Gonzales and Woods. Part of the problem is that the Convol function retains the same data type as the original image. But a true convolution with this kernal can result in negative image values. We are discarding such values when we displayed the filtered image, above. The proper way to do the convolution is to make both the filter and the image integer values. Then the filter can be scaled by subtracting the minimum value of the filter from the results, and then multiplying by 255 and dividing by the maximum value of the filter after the minimum value has been added to it. The code looks like this.

   IDL> filtered = Convol(Fix(image), kernel, Center=1)
   IDL> filtered = filtered - Min(filtered)
   IDL> filtered = filtered * (255.0/Max(filtered))
   IDL> TV, filtered

Note the use of "255.0" in the expression above. If I used a "255" I would be doing integer division and the result would undoubtably be a zero, not what I expect. One side effect of this is that the filtered image is now a floating point array, even though it is scaled in the range of 0 to 255. (The TV command converts the floating point array to byte values before it is displayed.)

You see the scaled filter results in the figure below.

Now, to complete the image sharpening I have to add the filtered Laplacian image back to the original image, and scale the data into the range 0 to 255. Here is the code.

   IDL> sharpened = image + filtered
   IDL> sharpened = sharpened - Min(sharpened )
   IDL> sharpened = sharpened * (255.0/Max(sharpened ))
   IDL> TV, sharpened

The sharpened image is shown below. Note the presence of more fine detail in the image.

The sharpened image is quite a bit lighter than the same image shown in Gonzales and Woods. But I think this is because the image doesn't have the same dynamic gray-scale range as the original image. A quick histogram stretch (done with cgStretch) quickly puts things right. By stretching the image between the values 60 and 200, we come up with the final image, shown below beside the original image.

   IDL> TV, BytScl(sharpened, Min=60, Max=200)

If you would like to try Laplacian sharpening with your own image, you can use the Sharpen program. Rather than stretching the image as above, the Sharpen program matches the histogram of the sharpened image to the histogram of the original image with the Histomatch program. You would use it like this to obtain a sharpened image.

   IDL> sharpenedImage = Sharpen(image)

If you would like to see the intermediate steps, set the Display keyword.

   IDL> sharpenedImage = Sharpen(image, /Display)