Calculating Derivatives in IDL
QUESTION: I'm having trouble understanding how to calculate derivatives in IDL using the DERIV function? For example, suppose I create a data set like this:
data = Findgen(100) y = 0.95 * Sin(data/5)
I know that the derivative of Sin(X) is Cos(X), so I would expect if I plot DERIV(Y) I should see a cosine function.
Plot, y dx = DERIV(y) OPlot, dx, LineStyle=2
In fact, I do, but the scale is vastly smaller than what I expect. How come?
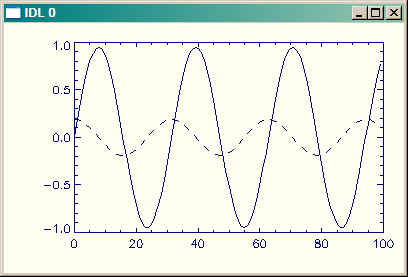 |
| The derivative is correct, but seems to be on the wrong scale. Why? |
![]()
ANSWER: We know, by the chain rule that:
d/dx(f(g(x))) = f'(g(x))*g'(x)
So, in your case:
d/dx(Sin(data/5)) = Cos(data/5) * (1/5)
The left-hand side of this equation is DERIV(Y), so you can see that if you simply multiply your answer by 5 that you will have what you want.
Plot, y dx = DERIV(y) OPlot, dx * 5, LineStyle=2
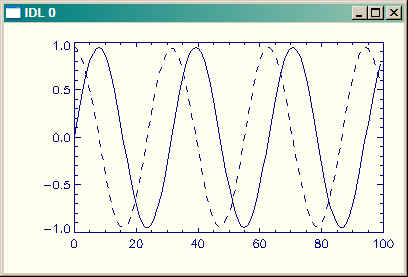 |
| Now the derivative is plotted at the correct scale. |
Another way to find the correct answer would be to pass the function you are differentiating to the DERIV function, like this:
data = Findgen(100) y = 0.95 * Sin(data/5) Plot, y dx = DERIV(data/5, y) OPlot, dx, LineStyle=2
Or, even better, perform the division first, like this:
data = Findgen(100) / 5 y = 0.95 * Sin(data) Plot, y dx = DERIV(data, y) OPlot, dx, LineStyle=2
![]()
Copyright © 2006 David W. Fanning
Last Updated 16 October 2006
