Finding the Convex Hull of a Set of Points

QUESTION: I have an arrays of X and Y data and I want to plot a polygon or outline that encompasses all the points. Can you show me how to do this?

ANSWER: The easiest way to determine the perimeter or convex hull of a set of data is with the Triangulate procedure. The fourth positional parameter, named hull in the program below, is an output variable that returns a vector of the data indices that constitute the perimeter.

Here is an example using data supplied by an IDL newsgroup reader.

   PRO Convex_Hull

      ; Create the example data set.

   x=[0.36,0.35,0.39,0.42,0.60,0.41,0.48,0.73,0.46, $
      0.42,0.42,0.42, 0.47,0.44,0.47,0.49,0.54,0.64,0.65]
   y=[0.19,0.26,0.26,0.26,0.14,0.22,0.15,0.10,0.16,$
      0.30,0.27,0.27,0.23,0.23,0.22,0.16,0.16,0.08,0.08]
         
      ; Load some display colors.
      
   TVLCT, [0,255,100], [255,255,100], [0,0,100], 1
   Device, Decomposed=0

      ; Plot the data, surrounded by the perimeter or
      ; convex hull.
      
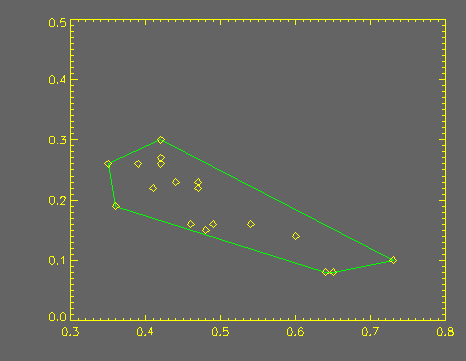
   Plot, x, y, Color=2, /NoData, Background=3, YRange=[0.0,0.5]
   Triangulate, x, y, triangles, hull
   PlotS, [x[hull],x[hull[0]]], [y[hull],y[hull[0]]], Color=1
   PlotS, x, y, PSym=4, Color=2

   END

The output of the program looks like the illustration below.