Increase the Speed of Krig2D




QUESTION: I've heard on the grapevine that it is possible to increase the speed of Krig2D by an order of magnitude. Is this true?
![]()
ANSWER: Apparently so. Michele Cappellari discovered a mathematically equivalent expression in Krig2D that speeds this extremely slow function up by at least an order of magnitude. As of IDL 8.2.3, you should findthe following lines of code in the krig2d.pro file (found in the IDL lib directory).
for j=0,ny-1 do begin ;Each output point
y0 = bounds[1] + gs[1] * j
for i=0,nx-1 do begin
x0 = bounds[0] + gs[0] * i
d[0] = reform(sqrt((x-x0)^2 + (y-y0)^2),n) ;distance
d = call_function(fname, d, t) ;Get rhs
d[n] = 1.0 ;lagrange constr
d=LUSOL( a, indx, d) ;Solve using LUDC results.
r[i,j] = total(d * z)
endfor
endfor
Replace this code with the following lines, which essentially just moves the LUSOL call outside the double FOR loop and changes the order of the array operations. According to Michele, this works because array multiplication is cummutative.
az = LUSOL(a, indx, [z,0.0]) ;Solve using LUDC results.
for j=0,ny-1 do begin ;Each output point
y0 = bounds[1] + gs[1] * j
for i=0,nx-1 do begin
x0 = bounds[0] + gs[0] * i
d[0] = reform(sqrt((x-x0)^2 + (y-y0)^2),n) ;distance
d = call_function(fname, d, t) ;Get rhs
d[n] = 1.0 ;lagrange constr
r[i,j] = total(d * az)
endfor
endfor
Michele supplies the following example routine, which is more than 30 times faster than the unmodified code and more than seven times faster than the built-in (and presumably optimized) GridData code, which suggests that GridData is making the same mistake and can be made faster, too, although not by users.
; Create a dataset of N points.
n = 500 ;# of scattered points
seed = -121147L ;For consistency
x = RANDOMU(seed, n)
y = RANDOMU(seed, n)
; Create a dependent variable in the form a function of (x,y)
z = 3 * EXP(-((9*x-2)^2 + (7-9*y)^2)/4) + $
3 * EXP(-((9*x+1)^2)/49 - (1-0.9*y)) + $
2 * EXP(-((9*x-7)^2 + (6-9*y)^2)/4) - $
EXP(-(9*x-4)^2 - (2-9*y)^2)
s = [0.5,0]
tic
z2 = krig2d_modified(z, x, y, EXPONENTIAL=s, NX=200, NY=200)
toc
tic
z2 = GRIDDATA(x, y, z, /KRIGING, DIMENSION=[200,200], VARIOGRAM=[2,s])
toc
tic
z2 = krig2d(z, x, y, EXPONENTIAL=s, NX=200, NY=200)
toc
END
![]()
Further Enhancements
The folks at ExelisVis got right on this, but they discovered a further problem. The Krig_Sphere function code in Krig2D doesn't match the documentation, and there appears to be a problem with the code itself.
Eventually, things got sorted out and ExelisVis posted a new Krig2D_Fast program on the IDL newsgroup. Running Michele's example code with the new program was about 80 times faster than the original IDL Krig2D program on my computer! Similar code has been added to the GridData program and will make that program much faster at Kriging in IDL 8.3. Here are the results as reported by ExelisVis:
Old KRIG2D: 30 seconds New KRIG2D: 0.51 seconds New GRIDDATA: 1.3 seconds
Note, too, that Michele reports the "new covariance functions now looks right and corrects for some major numerical differences one can see against the old Krig2D, when the data extend beyond the region where the semivariogram was supposed to flatten out."
 |
| The 2D result of the fast Kriging algorithm. |
![]()
Coyote Kriging Program
Because I wanted to have a kriging function that I could use with all versions of IDL, and because I wanted to learn more about kriging in general, I decided to write my own Krig2D function, which I called cgKrig2D. I decided in my function to use semivariograms rather than covariance matrices, and I modified the kriging models appropriately. I also added additional error handling and I discovered and fixed a problem with the original Krig2D command that was always confusing to me. Namely, whenever I used a 2D grid as input to the function, I seemed to get nonsense values back. I never understood why.
It turns out that when kriging a 2D grid that you must match the size of the input grid with the size of the output grid. This is not mentioned in the documentation. Here is an example of what I mean.
inputGrid = Dist(11) outputGrid = Krig2D(inputGrid, Spherical=[5.0, 0.0]) !P.Multi=[0,2,1] cgDisplay, 1200, 450 cgSurf, inputGrid cgSurf, outputGrid !P.Multi=0
You see the result of this code in the figure below.
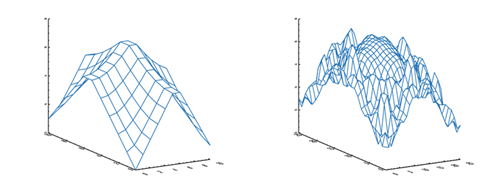 |
| If the dimensions of the input and output grid are not matched, chaos ensues. |
inputGrid = Dist(11) outputGrid = cgKrig2D(inputGrid, Spherical=[5.0, 0.0]) !P.Multi=[0,2,1] cgDisplay, 1200, 450 cgSurf, inputGrid cgSurf, outputGrid !P.Multi=0
You see the result of this code in the figure below.
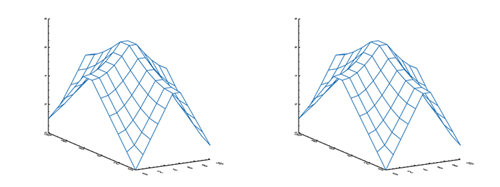 |
| The cgKrig2D program makes sure dimensions of gridded data are matched. |
![]()
Version of IDL used to prepare this article: IDL 8.2.3.
![]()
![]()







